Research

My research is focused on the numerical solution of Einstein's equations. Due to the highly nonlinear and complex nature of these equations only a few analytic solutions have been found since the theory of general relativity was published in 1915. This has spurred the development of the field of numerical relativity wherein large scale computing is used to model scenarios where the gravitational field is very strong and time-dependent.
Many studies in numerical relativity concentrate on the interactions of strongly gravitating objects---such as a black holes or neutron stars---that are of astrophysical relevance, particularly in the context of the generation and detection of gravitational radiation. However, a computational approach can also be used to study fundamental issues in gravitational theory, and my work is in that spirit. Among the predictions of Einstein's theory the existence of black holes and the singularities that may arise at their centers are among the most peculiar and interesting in theoretical physics. Pioneered by my supervisor (Choptuik), numerical investigations of the collapse of matter at the threshold of black hole formation have shown that the nonlinearity of Einstein's equations can lead to surprising structure which is analogous to critical phenomena in statistical mechanical systems. In addition, the critical behaviour seen at the black hole threshold describes evolution from a smooth initial matter configuration to a spacetime with divergent curvature that can be seen by distant observers. This provides examples of naked singularities, which in turn are related to other fundamental investigations in quantum gravity and cosmology.
My research concentrates on the study of this critical phenomena in the collapse of star clusters and the pure strong gravity wave. The key computational task is to solve a complex set of time-dependent nonlinear PDEs using finite difference and finite volume methods, high performance computing facilities and advanced algorithms including adaptive mesh techniques. The latter are crucial in resolving the intricate, small-scale structures that typically arise in critical collapse, and to do so in a computationally efficient way. Another central element of my work involves exploitation of the coordinate freedom inherent in general relativity to design coordinate systems that adapt to possible emerging symmetries in the solutions: this can lead to further increases in computational efficiency.
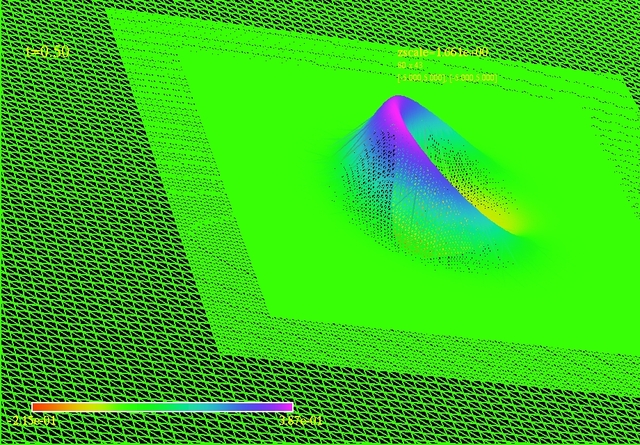
Evolution of Strong Non-linear Gravity Wave:
Evolution of pure strong gravity wave in axial symmetry. Part of the wave package disperses toward the outer radius, while the ingoing part approaches the center and creates a highly curved spacetime. The twisted vacuum eventually collapses to a blackhole. Calculations are performed on a nonuniform grid in cylindrical coordinate. The plot is the \(\tilde{\gamma}_{zz} \) component of the conformal metric. Typical calculations are of order 24h x 32CPU on a 512 x 1024 non-uniform grid structure.Particularly, the last snapshot demonstrates the formation of a blackhole as the gravitational wave concentrates in the vicinity of the origin and gets trapped by its own gravity.
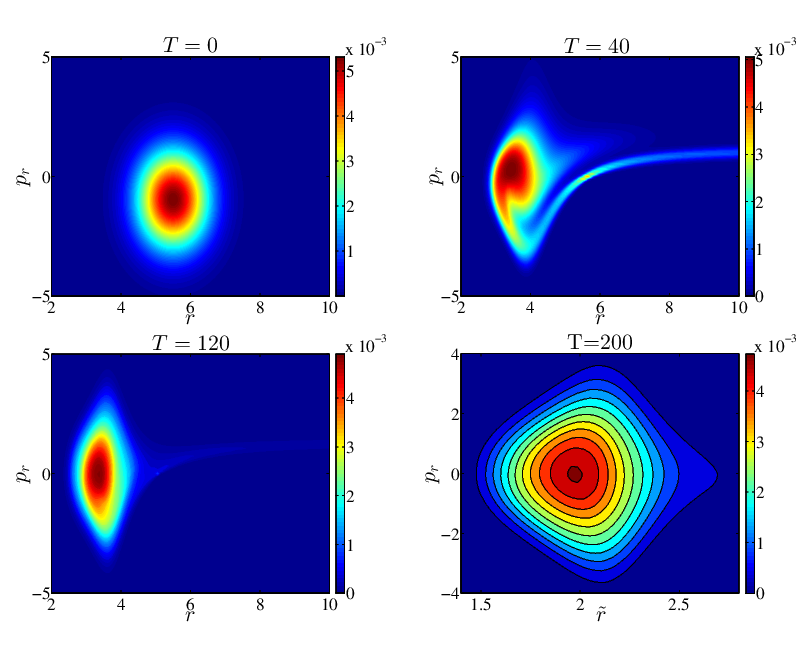
Phase Space Evolution of Einstein-Vlasov System:
Phase space evolution of the particle distribution function \( f(t,\vec{x},\vec{p}) \) for Einstein-Vlasov system in a strongly self gravitating scenario. The initial distribution describes a set of localized particles with average ingoing momentum (imploding shell of particles). In the early stages of the evolution we observe phase space mixing and the ejection of some particles ( visible as a tail in the second frame).At the intermediate times, the system approaches a static state which persists for a period that is much longer compared to the timescale characterizing weak field dynamics. This initial data is tuned such that it is (upto machine precision) at the precise criticality, i.e. the system neither collapses to a blackhole nor disperses to infinity. This meta-stable state is characterized as Type I critical phenomena in gravitational collapse. We note that this is a 3D calculation, with \( f \) non-trivial in the angular momentum \( l \) direction: for visualization purposes we have integrated over \( l \) to produce a quantity depending only on radial direction and radial momentum. See: http://arxiv.org/abs/1409.5176