Publications:
Black hole critical behaviour with the generalized BSSN formulation
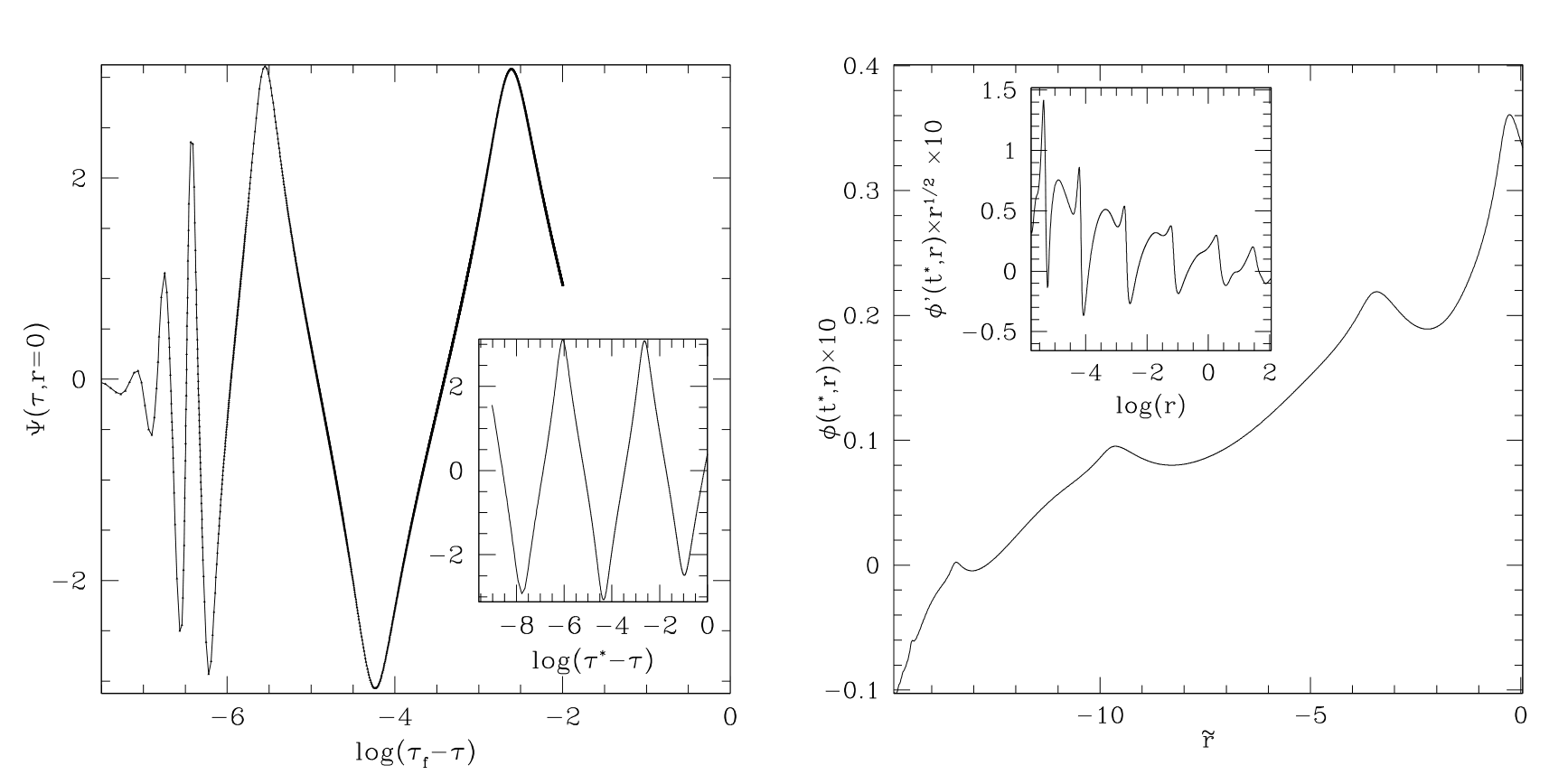
Development of discrete self similarity in the scalar field and geometry at the threshold of blackhole formation.
Abstract:
The development and use of hyperbolic formulations of Einstein's equations has revolutionized our ability to perform long-time, stable, accurate numerical simulations of strong field gravitational phenomena. However, hyperbolic methods have seen relatively little application in one area of interest, type II critical collapse, where the challenges for a numerical code are particularly severe. Using the critical collapse of a massless scalar field in spherical symmetry as a test case, we study a generalization of the Baumgarte-Shapiro-Shibata-Nakamura (BSSN) formulation due to Brown that is suited for use with curvilinear coordinates. We adopt standard dynamical gauge choices, including 1+log slicing and a shift that is either zero or evolved by a Gamma-driver condition. With both choices of shift we are able to evolve sufficiently close to the black hole threshold to 1) unambiguously identity the discrete self-similarity of the critical solution 2) determine an echoing exponent consistent with previous calculations 3) measure a mass scaling exponent, also in accord with prior computations. Our results can be viewed as an encouraging first step towards the use of hyperbolic formulations in more generic type II scenarios, including the as yet unresolved problem of critical collapse of axisymmetric gravitational waves.
e-Print: arXiv:gr-qc/1508.01614 
Phys. Rev. D.92, 084037, (2015) 
Critical collapse in the spherically-symmetric Einstein-Vlasov model
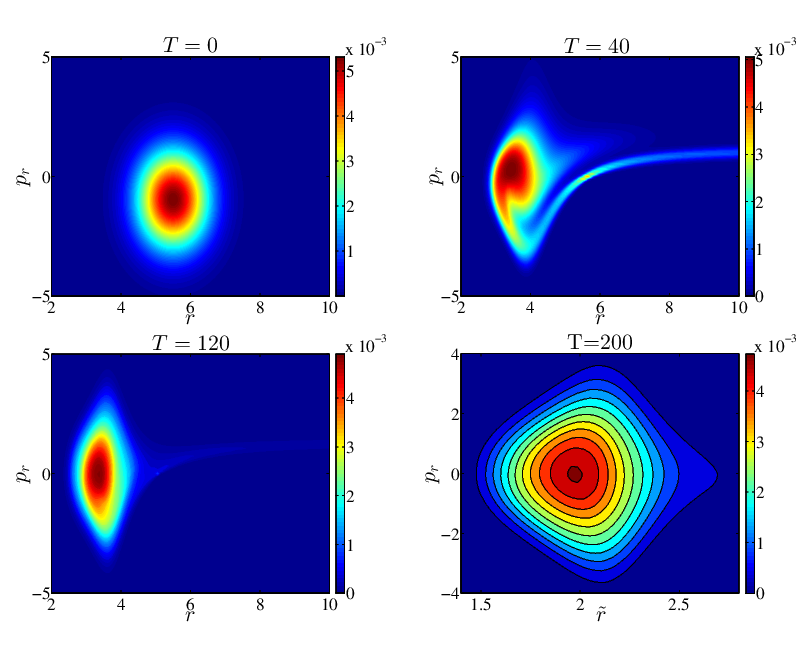
The sub-critical solution in Einstein-Vlasov system. Here the function is presenting the distribution of the particles in phase space and the final state is approaching a static configuration.
Abstract:
We solve the coupled Einstein-Vlasov system in spherical symmetry using direct numerical integration of the Vlasov equation in phase space. Focusing on the case of massless particles we study critical phenomena in the model, finding strong evidence for generic type I behaviour at the black hole threshold that parallels what has previously been observed in the massive sector. For differing families of initial data we find distinct critical solutions, so there is no universality of the critical configuration itself. However we find indications of at least a weak universality in the lifetime scaling exponent, which is yet to be understood. Additionally, we clarify the role that angular momentum plays in the critical behaviour in the massless case.
e-Print: arXiv:gr-qc/1409.5176 
Phys. Rev. D.90, 104023, (2014) 
FD: Finite Difference Toolkit

Screenshot of an FD (Maple) script that creates a solver routine for 1D heat equation, as well as a routine to set the initial temperature profile.
FD is a toolkit for finite difference methods used in solving Partial Differential Equations (PDE). Specifically, it is a set of Maple tools that provides a high level language to define a PDE over a discretized numerical domain and solve it. This toolbox can compute the Finite Difference Approximation (FDA) equivalent of a PDE and generate low level language (Fortran) routines and C wrappers to evaluate the FDA expression or solve it for the dynamical (unknown) field. The process of posing a PDE as an FDA expression has several complications, including finding the proper terms for derivatives with correct accuracy, handling boundary points, initialization, developing testing facilities and generating solver routines. FD is designed to simplify these steps while allowing full control over the entire process and helps the user to focus on the underlying physical/mathematical phenomena described by the PDE. It also provides a rapid prototyping language to apply various discretization schemes, test the desired accuracy and develop a solid set of routines that are parallel ready and can be used within a framework of a parallel computing infrastructure such as PAMR.
[User Manual 
 ]
]
[Software Documentation Page  ]
]
Relative Stability in Critical Collapse of Two Scalar Fields with Angular Momentum
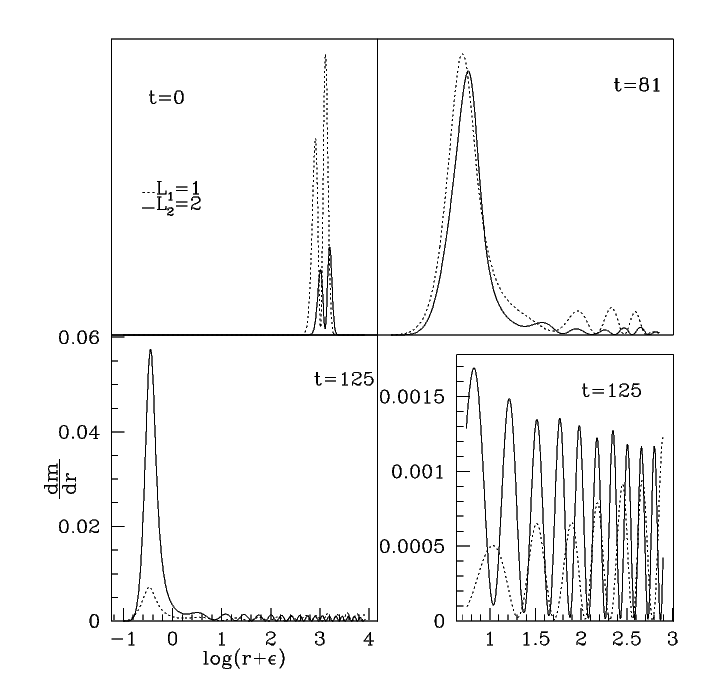
The interaction of two matter fields at the threshold of blackhole formation.
Abstract:
We study numerically the gravitational collapse of two massless scalar fields in spherical symmetry using an approach which incorporates some of the effects of angular momentum. Each field is characterized by a distinct angular momentum parameter, \( l \), with \(l = 0, 1, 2, \ldots\) and has distinct equations of motion. We focus on black critical behaviour, in which we look for solutions, and the properties thereof, that represent the onset of black hole formation in parametrized families of initial data. Although many different critical solutions have been discovered since the early 1990's, almost all work has involved a single matter source, and by coupling more than one type of matter to the gravitational field, new and interesting questions arise.
In particular, we consider the issue of the relative stability of the critical solutions in our model, in which we look for signs of instability of one field in the presence of the critical solution associated with the other. Our main result is that fields corresponding to larger values of \(l\) appear to be unstable in the context of lower-\(l\) critical solutions. This implies that in a two-field universe, the field with larger \(l\) would always dominate at precise criticality.
[Full text, via UBC circle  ]
]