Numerical Relativistic Hydrodynamics

Hydrodynamics allows for an effective description of macroscopic matter providing the matter is in local thermal equilibrium.

$\begin{displaymath} P = (\Gamma-1)\rho_0\epsilon \end{displaymath}$

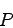
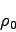
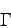
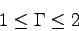$\begin{displaymath}P\end{displaymath}$ $\begin{displaymath}\rho_0\end{displaymath}$ $\begin{displaymath}\epsilon\end{displaymath}$ $\begin{displaymath}\Gamma\end{displaymath}$ $\begin{displaymath}1\le\Gamma\le 2\end{displaymath}$ Therefore the state of a patch of fluid is fully described by a set of position dependent state variables (i.e. fields). The evolution of these fields is governed by the relativistic Euler's equations. In addition to the equations of motion one must supply the eqaution of state. The equation of state for the ideal fluid has the form where is the isotropic pressure is the rest mass density and is the specific internal energy. is the adiabatic index (). Euler's equations constitute a set of hyperbolic partial differential equations. By specific choice of variables these equations can be written in conservative form (possibly with sources). It is well known that solutions of the Euler's equations generically develop discontinuities even from initially smooth data. One can either smooth the discontinuities by introducing an artificial viscosity or use a different method for solving the hydrodynamic equations - the so called high resolution shock capturing methods (HRSC). In recent years the latter approach became increasingly more popular. HRSC methods are based on a different type of discretization - the so-called finite volume discretization. Here instead of approximating the value of a field variable at a grid point one evolves the volume average of the field over a computational cell. One then calculates the fluxes of the conservatives fluid variables over all of the cell boundaries and then adjusts the cell averages accordingly (if sources are present their contribution is also included) Since the Einstein equations are most often solved with finite difference approximation it is not straightforward to incorporate matter into the calculations. I am currently involved in a collaborative effort with Frans Pretorius to include the HRSC hydro solver into his parallel adaptive mesh refinment infrastructure (PAMR/AMRD). More about this can be found here.
In some cases one can assume that the fluid is not coupled to gravity (a test fluid) and only moves in a prescribed geometry. This geometry is typically a static or stationary solution of Einstein's eqautions such as Minkowski, Schwarzschild or Kerr spacetime. This approach has been successfully used to simulate astrophysical jets, wind accretion onto black holes and accretion disc around black holes. In order to familiarize myself with the HRSC methods in the framework of GR I have developed a code which can evolve relativistic ideal fluid in a background geometry in 1D,2D (spherical symmetry, axisymmetry) and 3D. The code can run in a parallel environment (using PAMR) and performs well on a Linux Beowulf cluster.

Astrophysical Jets

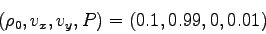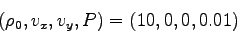Jets are ubiquitous in extragalactic radio sources associated with active galactic nuclei. Although to explain their origin GR magnetohydrodynamics is needed, to study the morphology of the jet a SR hydrodynamics is sufficient. The following is a simulation of a 2D planar jet ( $\begin{displaymath}(\rho_0,v_x,v_y,P)=(0.1,0.99,0,0.01)\end{displaymath}$ ) moving through an extragalactic medium ( $\begin{displaymath}(\rho_0,v_x,v_y,P)=(10,0,0,0.01)\end{displaymath}$ ). 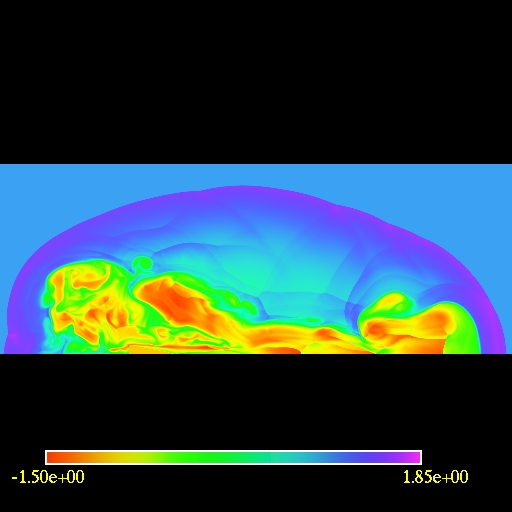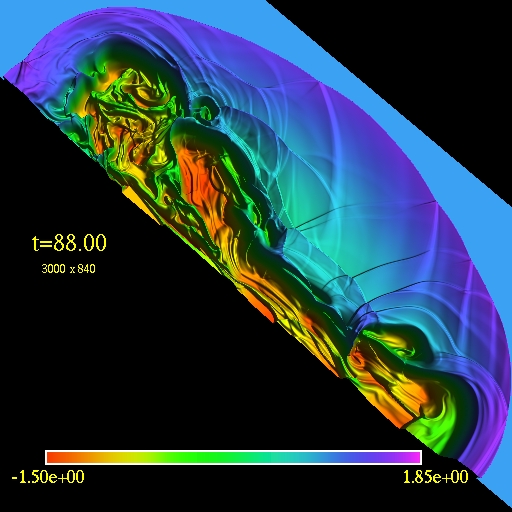The first image/movie below shows the log of the fluid density of a the jet. The second image/movie shows a 3D view of the domain. In order to visualize the fluid flow one can trace test particles trajectories. I started with random uniform particle distribution and regularly added particles into the jet source. The third image/movie shows the motion of the tracers. Since the jet is symmetric it is sufficient only to use half of the domain for calculations and to use reflection boundary conditions at the symmetry axis. The computational domain is (-20,55)x(0,21) and the resolution is 3000x840 cells.
Note the presence of an external bow shock and the vortices due to the Kelvin-Helmholtz instability.


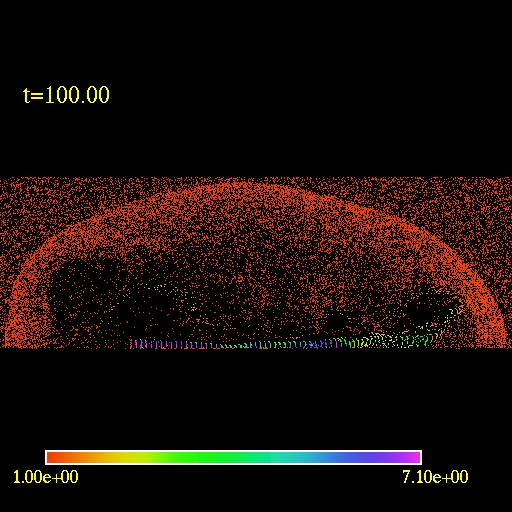2D view of the computational domain. Logarithm of the fluid density is plotted. (click to play mpeg movie)	3D view of the computational domain. Logarithm of the fluid density is plotted. (click to play mpeg movie)	Visualization of the fluid flow by trace particles. (click to play mpeg movie)

Wind Accretion onto Black Hole

These are the results of simulations of a relativistic wind accretion onto a Schwarzschild BH. The models are taken from the paper by Font et. al.
A NUMERICAL STUDY OF RELATIVISTIC BONDI-HOYLE ACCRETION ONTO A MOVING BLACK HOLE:AXISYMMETRIC COMPUTATIONS IN A SCHWARZSCHILD BACKGROUND,494,297-316 (1998)

Here is the table from the paper describing the models (I think that r_min(r_a) for model MC2 should be 0.57 - 0.44 would be below the Schwarzschild radius)

TABLE 1
INITIAL MODELS
Model	cs_∞	G	Μ_∞	v_∞	r_a(M)	r_min(r_a)	r_max(r_a)	t_f(M)
MA1...	0.1	1.1	1.5	0.15	30.8	0.125	10.0	4000
MA2...	0.1	1.1	5.0	0.5	3.8	0.57	10.0	750
MB1...	0.1	4/3	1.5	0.15	30.8	0.125	10.0	4000
MB2...	0.1	4/3	5.0	0.5	3.8	0.57	10.0	750
MC1...	0.1	5/3	1.5	0.15	30.8	0.125	10.0	2000
MC2...	0.1	5/3	5.0	0.5	3.8	0.44	10.0	750
UA1...	0.31	1.1	1.5	0.47	3.2	0.69	9.38	200
UA2...	0.31	1.1	3.0	0.93	1.04	2.12	28.85	110
UB0...	0.57	4/3	0.6	0.34	2.2	1.0	13.64	200
UB1...	0.57	4/3	1.5	0.86	0.92	2.39	32.61	200
UC0...	0.81	5/3	0.6	0.49	1.1	2.0	27.27	200

cs_∞	asymptotic sound speed (i.e., at the outer boundary)
G	adiabatic exponent
Μ_∞	asymptotic Mach number at infinity
v_∞	asymptotic flow velocity
r_a(M)	accretion radius
r_min(r_a)	inner boundary in units of accretion radius
r_max(r_a)	outer boundary in units of accretion radius
t_f(M)	final time at which the simulation was stopped


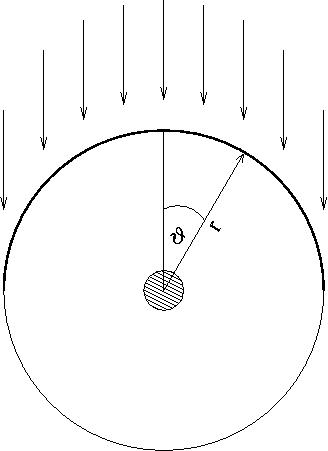	Wind accreation schematics. The outer circle is the outer boundary. The small circle in the middle represents the inner boundary with the black hole.

First is the simulation of the model MC2 performed on a 200x100 grid (r,theta) using Eddington-Finkelstein ingoing coordinates. The grid is logarithmic in r-direction and uniform in theta. The inner radius is located at r=1.75M and the outer radius is at r=100M. In this simulation (unlike in the paper) I put vacuum in the whole domain except at the ghost zones in the upper hemisphere at initial time. The vacuum was a true vacuum, i.e., all the variables were set to zero. It is a bit tricky to evolve such a setup but the method I implemented seemed to work fine. Since this is log₁₀ plot I added 1.e-3 to the density so vacuum would be represented by the value -3.


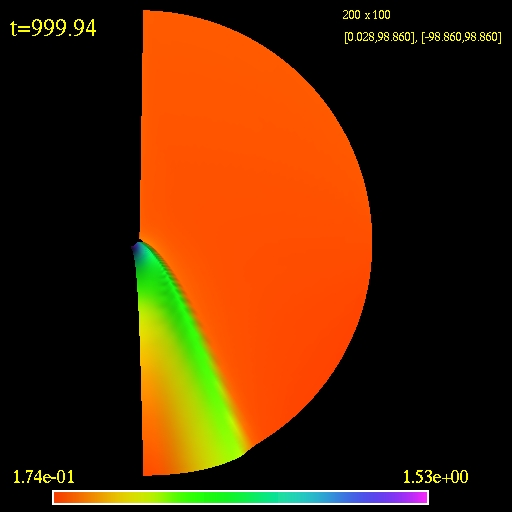
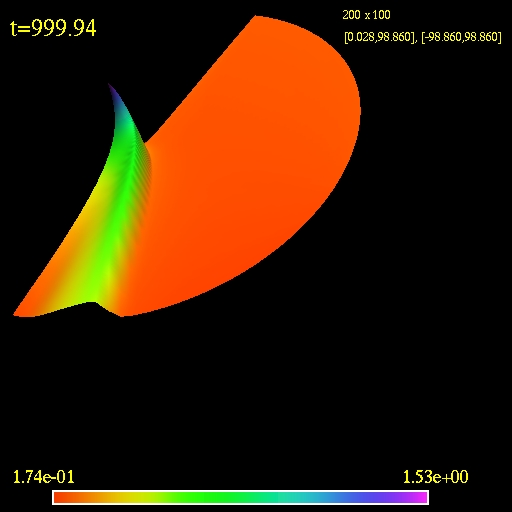2D view of the computational domain. Logarithm of the fluid density is plotted. (click to play mpeg movie)	3D view of the computational domain. Logarithm of the fluid density is plotted. (click to play mpeg movie)

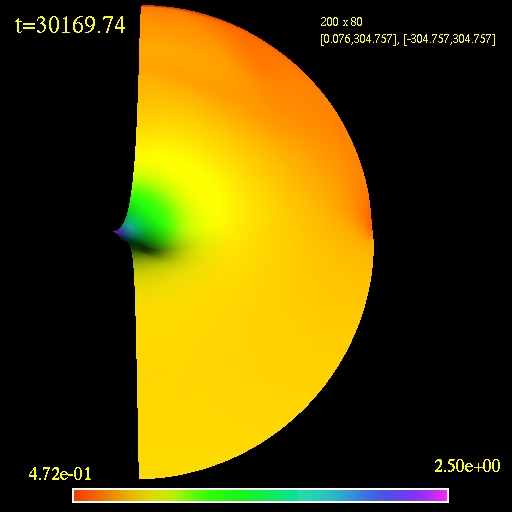
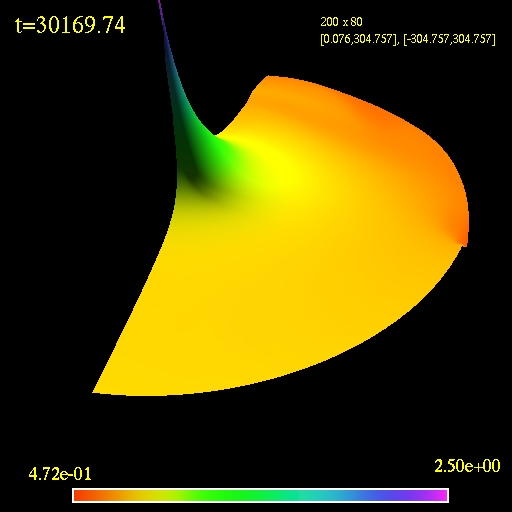
The next simulation is for the model MB1. This particular one is done in Schwarzschild coordinates but the results do not change when using Eddington-Finkelstein ingoing coordinates. The simulation shows that if a stationary state is reached it would be qualitatively different than the one for the model MC2 which is unexpected. I performed many simulations in both types of coordinate systems with different resolutions, domain sizes and flux approximations. All result in the same behaviour, i.e., the detachment of the initially formed shock and its dispersion. My computed accretion rates for all tested models agree to those published until the t_f(M) for each simulation. My evolution of the model MC1 shows similar behaviour - a hint of it might be even present in the paper - the simulation of C1 shows a detached shock but the simulation was stopped at t=2000M.


2D view of the computational domain. Logarithm of the fluid density is plotted. (click to play mpeg movie)	3D view of the computational domain. Logarithm of the fluid density is plotted. (click to play mpeg movie)

Accretion Discs

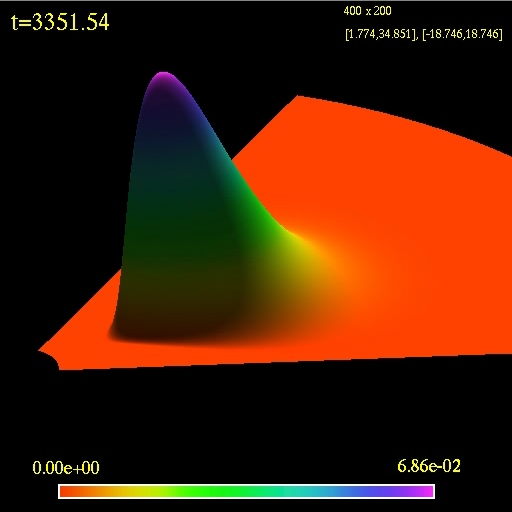
The most spectacular accretion discs in nature are found in active galactic nuclei and most probably at the center of quasars. It is thought that a super massive black hole is located at the center with matter orbiting around it and spiraling inwards. Below are two simulations of accretion discs around Schwarzschild black hole. The first image/movie shows an evolution of an stable accretion disc. All of the matter is inside its Roche lobe so no matter transfer should occur (a "numerical leak" can be seen at the end of the simulation).
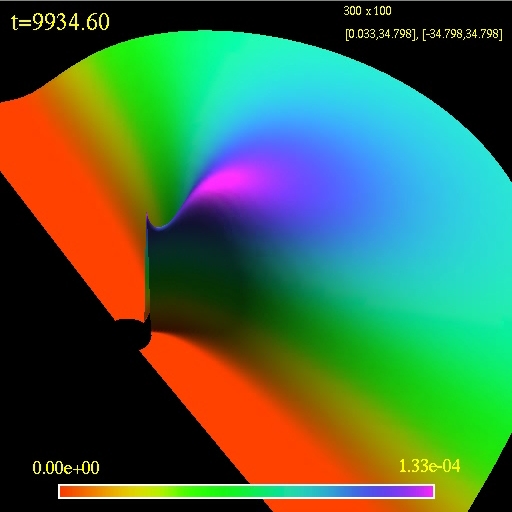
The second image/movie shows an evolution of a disc overflowing its Roche lobe. There is a steady matter flow into the black hole. The model s are taken from arxiv:astro-ph/0203403.


3D view of the computational domain. Logarithm of the fluid density is plotted. (click to play mpeg movie)	3D view of the computational domain. Logarithm of the fluid density is plotted. (click to play mpeg movie)